Quantifying Scatter
Written by: John C Stover
Scatter signals can be easily quantified as scattered light power per unit solid angle (in watts per steradian); however, in order to make the results more meaningful, these signals are usually normalized, in some fashion, by the light incident on the scatter source. The three ways commonly employed to do this (BRDF, TIS and DSC) are defined here.
Download: ![]() Quantifying-Scatter-PDF
Quantifying-Scatter-PDF
The bi-directional reflectance distribution function
If the feature in question is uniformly distributed across the illuminated spot on the sample (such as surface roughness), then it makes sense to normalize the scatter signal by the incident power. This simple ratio, which has units of inverse steradians, was commonly referred to as “angle resolved scatter” or the ARS. Although this term is still found in the literature, it has been generally replaced by a closely related function, the bi-directional reflectance distribution function (or BRDF), which is defined by forming the differential ratio of the sample radiance normalized by its irradiance. After some simplifying assumptions are made, this reduces to the original scattering function with a cosine of the polar scattering angle in the denominator. The BRDF, defined in this manner, has become the standard way to report angle-resolved scatter from features that uniformly fill the illuminated spot. We have NIST to thank for this basic definition and ASTM and SEMI to thank for a standard method of measurement. The cosine term results from the fact that NIST defined BRDF in radiometric terms.
![]()
The ARS is also sometimes referred to as the “cosine corrected BRDF” and is simply equal to the BRDF multiplied by the cosine of the polar scattering angle. Figure 1 gives the geometry for the situation, and defines the polar and azimuthal angles (θs and φs) as well as the solid collection angle (Ω). The BRDF has units of inverse steradians and is usually measured by moving a circular collection aperture in some path across the scattering hemisphere. Figure 1 also shows that transmissive scatter (BTDF) is defined in the same way.
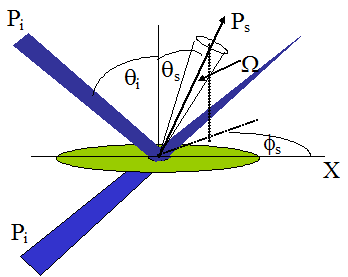
Figure 1. Standard spherical coordinates are used to define the geometry for the definitions of BRDF and BTDF.
Scatter Diffraction
Care has to be taken that the data is representative of the sample, or of the situation being investigated, as the scatter patterns of non-uniform and/or non-isotropic surfaces can exhibit a lot of structure. An extreme case is scatter (diffraction) from a grating which will produce a series of bright peaks in the hemispherical pattern. Scatter from surfaces scratches and steps will exhibit a streak of light. In cases where the pattern is dominated by a streak of light, it often makes sense to take the measurement using a slit aperture (perpendicular to the streak) and normalize by the slit width (Δθ in degrees) instead of the aperture solid angular area in steradians. These cases are called “one dimensional in nature because the surface frequencies associated with the feature “propagate” in only one direction. It is not reasonable to compare BRDF levels between one dimensional and two dimensional measurements. See Reference 1 for more details on these issues.
![]()
Integration of the scatter signal (or in effect the BRDF) over much of the scattering hemisphere allows calculation of the “total integrated scatter,” or TIS. This integration is usually carried out experimentally in such a way that both the incident beam and reflected specular beam are excluded. In the most common TIS situation, the beam is incident on the sample at normal (or near normal), and the integration is carried from small values of θs to almost 90 degrees. If the fraction of light scattered from the specular reflection is small and if the scatter is caused by surface roughness, then it can be related to the rms surface roughness of the reflecting surface. In this case, it makes sense to normalize the scatter measurement by the total reflected power, Pr, (or nominally the reflected specular beam for a smooth surface). As a ratio of powers, the TIS is a dimensionless quantity. This is done because reductions in scatter caused by low reflectance should not influence the roughness calculation. The pertinent relationships are given below, where σ is the rms roughness and λ is the light wavelength.
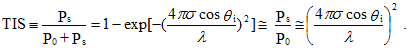
Of course all scatter measurements are integrations over a detector collection aperture, but the TIS designation is reserved for situations where the attempt is to gather as much scattered light as possible, while “angle resolved” designs are created to gain information from the distribution of the scattered light. Reference 1 discusses a number of subtleties associated with the TIS rms roughness relationship.
How to treat scatter from discrete features, such as particles and pits, which do not completely fill the illuminated spot.
Scatter from discrete features, such as particles and pits, which do not completely fill the illuminated spot, must be treated differently. This is because changes in spot size, with no corresponding change in total incident power, will change the incident intensity (watts/unit area) at the feature and thus the scatter signal (and BRDF) will change without any relation to changes in the scattering feature. Clearly this is unacceptable if the object is to characterize the defect with its quantified scatter. The solution is to define another quantification term, known as the differential scattering cross-section (or DSC), where the normalization is the incident intensity at the feature. The units for DSC are area/steradian. Because this was not done in terms of radiometric units at the time it was defined, the cosine of the polar scattering angle is not in the definition. The same geometrical definitions found in Figure 1 also apply for the DSC. If the DSC is integrated over the solid angle associated with a collection aperture then the value has units of area. Because tightly focussed laser beams are often used as a source, the area is most commonly given in micrometers squared.
![]()
where A is the illuminated area.
Optimizing instrument designs
These three scatter parameters, the BRDF, the TIS and the DSC, are obviously functions of system variables such as geometry, scatter direction (both in and out of the incident plane), incident wavelength and polarization, as well as feature characteristics. It is the dependence of the scatter signal on these system parameters that makes the scatter models useful for optimizing instrument designs. It is their dependence on feature characteristics that makes scatter measurement a useful metrology tool.
A key point needs to be stressed. When applied appropriately, TIS, BRDF and DSC are absolute terms, not relative terms. The DSC of a 100 nm PSL in a given direction for a given source is a fixed value, which can be repeatedly measured and even accurately calculated from models. The same is true for TIS and BRDF values associated with surface roughness of known statistics. Scatter measuring instruments, like particle scanners or lab scatterometers, can be calibrated in terms of these quantities. As has already been pointed out, the user of a scanner will almost always be more interested in characterizing defects than in the resulting scatter values, but the underlying instrument calibration can always be expressed in terms of these three quantities. This is true even though designers and users may find it convenient to use other metrics (such as PSL spheres) as a way to relate calibration.
Related References
- Optical Scattering: Measurement and Analysis, John C. Stover, SPIE Press, BellinghamWA, 2012 Third Edition
- Calibration of Particle Detection Systems; John C. Stover; Chapter 21 in: Handbook of Silicon Semiconductor Metrology; Alain Diebold, Editor, Marcel Dekker, New York, 2001.
- Scatterometers; John C. Stover; Chapter 21 in Vol 2 of: Handbook of Optics; Michael Bass Editor, McGraw-HillNew York 1995.
